不移动植树问题技巧

8 月 09, 2023 公考笔试

0 0

不移动植树问题是植树问题的一类，是广东省考的特色以及高频考点之一，它是在植树问题基本理论的基础上又进行拔高的一类题型，但同样有独有的套路，今天我们就一起来学习一下不移动植树问题的公式以及相应的技巧。

【粉笔干货】

【知识点】不移动植树

例：道路原来安装（A+1）座路灯,每座路灯之间距离相同，之后安装（B+1）座路灯，每座路灯之间距离仍然相同，最多有（）座原来的路灯不需要移动。

题型特征：间隔距离发生改变

（1）求不移动的段数：

前后两次段数的最大公约数即为不移动段数

（2）求不移动棵数：

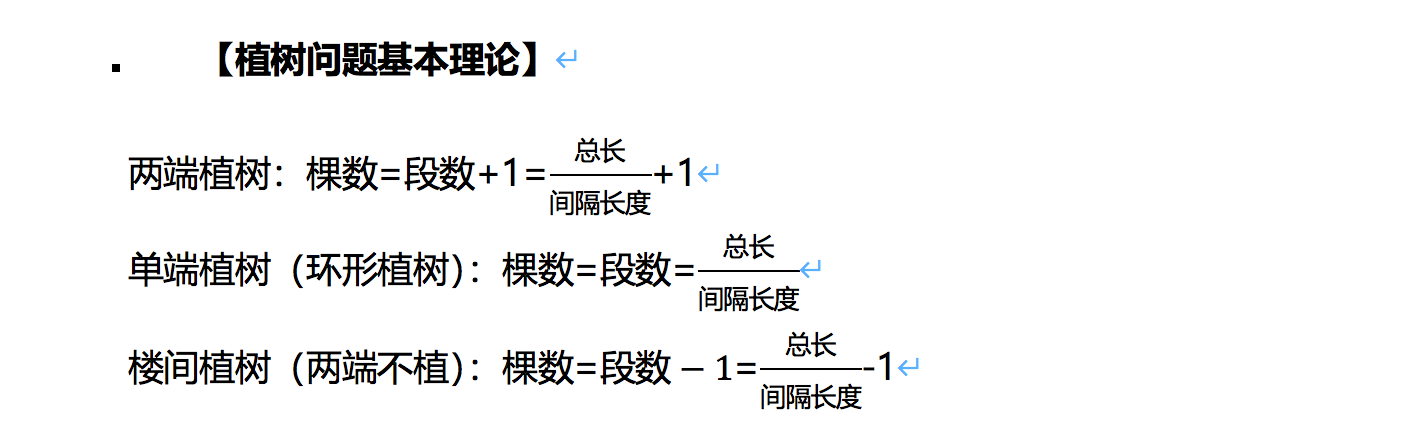
两端植树：棵数=不移动段数+1

单端植树（环形植树）：棵数=不移动段数

楼间植树（两端都不植）：棵数=不移动段数-1

真题示例

（2018广州）某条道路进行灯光增亮工程，原来间隔35米的路灯一共有21盏，现要将路灯的间隔缩短为25米，那么有（）盏路灯无需移动。

A. 2

B. 3

C. 4

D. 5

（3）求不移动棵数：

两端可以安装路灯，所以是两端植树，不移动路灯数量=不移动段数+1=4+1=5【选D】

（2017广东）施工队给一个周长为40米的圆形花坛安装护栏。刚开始，每隔1米挖一个洞用于埋栏杆。后来发现洞的间隔太远，决定改为每隔0.8米挖一个洞。那么，至少需要再挖几个洞？

A.39

B.40

C.41

D.42

【粉笔拓展】

1. 根据两头能否植树，分清是两端/单端（环形）/楼间

2. 注意是单侧植树还是两侧植树，两侧植树最后记得用一侧数量×2

【粉笔总结】