数资解题秒杀技:赋值法
在数量关系中,有些题目中具体数据给的不够,虽然可以通过设多个未知数求解,但是计算复杂会影响解题速度。因此我们可以通过赋值法来巧妙转化一下,避免设多个未知数,将复杂问题简单化,从而提高解题速度。赋值法容易学、可操作性强、运用范围广,是行测考试中节省时间的利器,因此大家要认真学习,多加练习。
01
适用范围:
(1)题干中没有出现具体的值,条件和问题都是以倍数、分数、比例、百分数的形式给出。
(2)在A=B×C这样的三量关系中,题干中至多给出其中一个量的具体值,其他的数据只是用比例关系表示甚至根本没有提到,则常用赋值的方法解决。
02
常见题型:
工程问题:总量=效率×时间
行程问题:路程=速度×时间
经济利润问题:总价=单价×数量 总利润=单利润×数量
浓度问题:溶质=溶液×浓度
平均数问题:总数=人数×平均数
03
具体用法:
若题干出现不变量,可考虑对不变量赋值,以连接所有题干条件,从而简化计算;
若解题时需要总量,比如工程总量、总路程、总价钱等,可考虑对总量赋值为题干所给部分量的公倍数;
若题干给出比例关系,比如效率之比、成本之比、销量之比、速度之比等,常结合比例关系赋值简单数,数字尽可能要便于计算和化简。
04
实际应用:
例1
(2020国考)
高架桥12:00~14:00每分钟车流量比9:00~11:00少20%,9:00~11:00、12:00~14:00、17:00~19:00三个时间段的平均每分钟车流量比9:00~11:00多10%。问17:00~19:00每分钟的车流量比9:00~11:00多:
A. 40% B. 50%
C. 20% D. 30%
【解析】
题干中只有百分数,求的也是百分数,因此可以赋值。根据“12:00~14:00每分钟车流量比9:00~11:00少20%…三个时间段的平均每分钟车流量比9:00~11:00多10%”,赋值9:00~11:00每分钟车流量为10,则12:00~14:00每分钟车流量为10×(1-20%)=8,9:00~11:00、12:00~14:00、17:00~19:00三个时间段的平均每分钟车流量为10×(1+10%)=11,则17:00~19:00每分钟车流量为11×3-10-8=15,(15-10)/10=50%,则17:00~19:00每分钟的车流量比9:00~11:00多50%。对应B项。【选B】
例2
(2016国家)
某集团有A和B两个公司,A公司全年的销售任务是B公司的1.2倍。前三季度B公司的销售业绩是A公司的1.2倍,如果照前三季度的平均销售业绩,B公司到年底正好能完成销售任务。问如果A公司希望完成全年的销售任务,第四季度的销售业绩需要达到前三季度平均销售业绩的多少倍?
A. 1.44 B. 2.4
C. 2.76 D. 3.88
【解析】
题干仅给出A、B两公司前三季度和全年的销售业绩倍数关系,故可根据倍数关系对两个公司的销售业绩赋值。因为主体多,列表梳理如下:
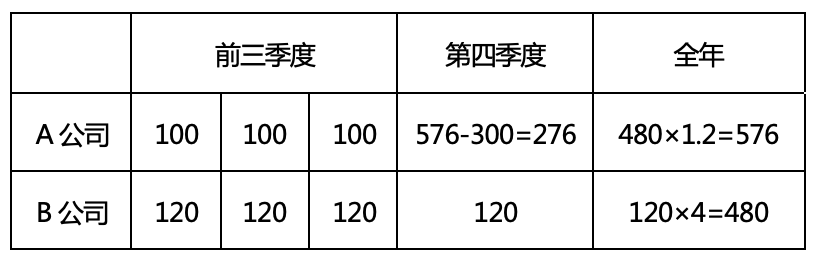
赋值A公司前三季度平均业务量为100,则B公司前三季度平均业务量为120,第四季度业务量也为120,故B公司全年业务量;根据A公司全年的销售任务是B公司的1.2倍,则A公司全年业务量, A公司第四季度业务量为,故题目所求倍。对应C项。【选C】
本站声明:网站内容来源于网络,如有侵权,请联系我们,我们将及时处理。

