国家开放大学:《几何基础》形考答案1-7
国家开放大学:《几何基础》形考答案
1、在仿射对应下,哪些量不变。( )
单选题(2 分)2分
A. 长度B.角度
C.单比D.交比
2、设共线三点 (0,2),B(2,0),C(11),则(ABC)=( ).单选题(2分)2分
A.1 B.-1
C.-2 D.2
3、下列叙述不正确的是( )。3
A.两个三角形面积之比是仿射变换下的不变量
B.三角形的重心有仿射不变性
C.样形在仿射对应下仍为样形
D.两个三角形边长之比是仿射变换下的不变量
4、正方形在仿射变换下变成( )。
A.正方形 B.平行四边C.菱形 D矩形
1、使三点 ![]() , ,
, ,![]() 分别变成点
分别变成点![]() , , 的仿射变换方程为( B )。
, , 的仿射变换方程为( B )。
A.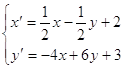 B.
B.
C. D.![]()
2.将点(2,3)变成(0,1)的平移变换,在这个平移下,抛物线 变成的曲线方程为( B )。
单选题 (4 分) 4分
A.![]() B.
B.![]()
C. D.![]()
3.使直线![]() 上的每个点不变,且把点(1,-1)变成点(-1,2)的仿射变换方程为 (B )。
上的每个点不变,且把点(1,-1)变成点(-1,2)的仿射变换方程为 (B )。
单选题 (6 分) 6分
A.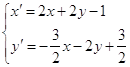 B.
B.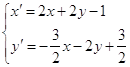
C. D.![]()
4.设 ![]() 和
和![]() 分别由
分别由![]() 和
和![]() 表示,则
表示,则![]() =( B )。
=( B )。
单选题 (6 分) 6分
A.![]() B.
B.
C.![]() D.
D.![]()
1.直线上的无穷远点的齐次坐标为( )。
单选题 (2 分) 2分
A.(1,1,0) B.(3,-1,0)
C.(1,-3,0) D.(3,1,0)
2.轴的齐次线坐标为( )。
A.[1,1,0] B.[0,1,0]
C.[1,0,0] D.[0,0,1]
3.y 轴上的无穷远点的齐次坐标为( ) 。
A.(0,1,0) B.(1,0,0)
C.(0,0,1) D.(1,1,1)
4.点(8,5,-1)的非齐次坐标为( )。
单选题 (2 分) 0分
A.(8,5) B.(-8,-5)
- (8,-5) D.无非齐次坐标
1、三角形ABC的二顶点A与B分别在定直线α和β上移动,三边AB,BC,CA分别过共线的定点P,Q,R,则顶点C( )。
A.在一定直线上移动
B.在P,Q,R所在的直线上移动
C.在B,Q所在的直线上移动
D.不能判定
2.设三角形ABC的顶点A,B,C分别在共点的三直线l,m,n上移动,且直线AB和BC分别通过定点P和Q,则直线CA( )。
单选题 (4 分) 4分
A.通过PQ上一定点
B.通过OP上一定点
C.通过OQ上一定点
D.不能判定
3.设P,Q,R,S是完全四点形的顶点,PS与QR交于A,PR与QS交于B,PQ与RS交于C,BC与QR交于A1,CA与RP交于B1,AB与PQ交于C1,则( )。
A.三直线AA1,BB1,CC1交于一点
B.A1,B1,C1三点共线
C.R,B1,C1三点共线
D.不能判定
1、设ΔABC的三条高线为AD,BE,CF交于M点,EF和CB交于点G,则(BC,DG)=( ).
单选题 (3 分) 3分
A.-1 B.1
C.2 D.-2
2.如果三角形中一个角平分线过对边中点,那么这个三角形是( ).
单选题 (3 分) 3分
A.等腰三角形 B.直角三角形
C.等边三角形 E.不能判定
1、下列叙述不正确的是( )。
单选题 (6 分) 6分
A.两线束间的射影对应是透视对应的充分必要条件是:两个线束的公共线自对应
B.共线四点的交比是射影不变量
C.不重合的两对对应元素,可以确定惟一一个对合对应
D.已知射影对应被其三对对应点所唯一确定,因此两个点列间的三对对应点可以决定唯一一个射影对应
2.巴卜斯命题:设A1,B1,C1与A2,B2,C2为同一平面内两直线上的两组共线点,B1C2与B2C1交于L,C1A2与C2A1交于M,A1B2与A2B1交于N.如下图,则得到( )。
单选题 (6 分) 6分
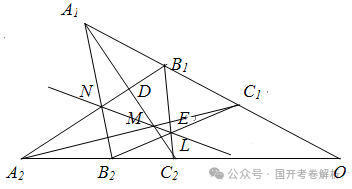
A.L,M,N共线
B.DC2,NL,A2E三直线共点M
C.(B1,D,N,A2)(B1,C2,L,E)
D.以上结论均正确
3.四边形ABCD被EF分成两个四边形AFED和FBCE,则三个四边形ABCD,AFED,FBCE的对角线交点K,G,H共线是根据( )定理得到。
图4-14
单选题 (6 分) 6分
A.笛沙格定理
B.巴卜斯定理
C.巴斯卡定理
D.布利安香定理
1.点(5,1,7)关于二阶曲线![]() 的极线为( C )。单选题 (5 分) 5分
的极线为( C )。单选题 (5 分) 5分
A.![]()
B.
C.![]()
D.![]()
2.直线关于二阶曲线![]() 的极点为( D )。单选题 (5 分) 5分
的极点为( D )。单选题 (5 分) 5分
A.(1,1,1)
B.(5,1,7)
C.(0,1,-1)
D.(-12,4,4)
3.若点P在二次曲线![]() 上,那么它的极线一定是
上,那么它的极线一定是![]() 的( A )。单选题 (1 分) 1分
的( A )。单选题 (1 分) 1分
A.切线
B.直径
C.半径
D.渐近线
4、二次曲线![]() 在点
在点![]() 处的切线方程为( D )。
处的切线方程为( D )。
单选题 (5 分) 5分
A.![]()
B.
C.![]()
D.![]()
5.无穷远点关于二次曲线的极线称为二次曲线的( B )。单选题 (1 分) 1分
A.切线
B.直径
C.半径
D.渐近线
6.二阶曲线![]() 是( A )。单选题 (1 分) 1分
是( A )。单选题 (1 分) 1分
A.抛物线
B.双曲线
C.实椭圆
D.虚椭圆
7.二阶曲线![]() 的中心及过点(1,1)的直径为( A )。单选题 (5 分) 5分
的中心及过点(1,1)的直径为( A )。单选题 (5 分) 5分
A.(-3, 1);![]()
B.( 3, 1);![]()
C.(-3, 1);
D.(1, 1);![]()
8.双曲线![]() 的渐近线方程为( D )。单选题 (5 分) 5分
的渐近线方程为( D )。单选题 (5 分) 5分
A.
B.![]()
C.![]()
D.![]()