特征数列是相对比较简单的数字推理题目，主要包括多重数列、分数数列、幂次数列、做商数列、图形数列五种数列形式。数字推理中的数字之间的规律虽然花样繁多，而特征数列的数字规律较为明显，外貌特征明显决定了这类题型易识别，只要考生把握每一种特征数列的关键特征和解题思路，考场之上从容应对特征数列是轻而易举。

1.多重数列

数列特征：数字多，项数多

解题思路：拆开看

（2015江苏A）2.3、4.8、8.24、16.51、32.89、（  ）

A. 64.138

B. 64.136

C.128.138

D.128.136

解题思路：数字比较多，拆开看。小数点前面的整数部分数列为：2、4、8、16、32，为公比为2的等比数列，下一项的整数部分是64。小数点后面的小数部分为：3、8、24、51、89，做差之后为5、16、27、38，为公差11的等差数列，下一项的小数部分为89+49=138。因此下一项为64.138。故本题正确答案为A。

多重数列是江苏省考广东省考和浙江省考都会考查相对较多的知识点，基本上每年都会看到多重数列的身影。对于多重数列的解题思路，我们已经介绍过：“拆开看”。考生还需要掌握的是如何来拆。

针对题干数字均是整数且数字较小，项数较多的数列，常见的拆分方法有奇数项看作一个数列，偶数项看作一个数列，以此分别寻找规律。或者数列两两来看，寻找规律；

针对题干数字较多，且数字位数较大的数列，一般是把数字拆开来看。

例如，1312、1715、2118、2521、2924、3327，数字较多且位数较大，此时的解题思路是四位数拆做前两位和后两位，变成数列13，17，21，25，29，33和12，15，18，21，24，27，再分别找出相关规律解题；针对题目出现分隔符的多重数列，一般是以分隔符为标准拆分数列。常见的分隔符有小数点，根号，除号。

2.分数数列

数列特征：分数的个数比较多；

解题思路：分子分母有关系，上下加减找规律。分子分母无关系，上下分别成规律，根据趋势反约分。

（2015江苏A）4，2，11/5，19/7，10/3，（）

A. 37/11

B. 4

C. 21/13

D. 5

解题思路：数列中分数与整数，考虑反约分。因为第三项和第四项分母为5和7，考虑将第五项分母转化为9，即30/9。再将第一项和第二项转换为分母为1和3的形式，数列变为4/1，6/3，11/5，19/7，30/9，分母为奇数列，下一项分母为11。分子数列做差之后为2，5，8，11，是公差为3的等差数列，下一项分子为30+14=44。则下一项为44/11=4。故本题答案为B。

分数数列也难度不是特别大，考生看到分数数列，先看分子与分母之间是否存在规律？再看分子之间或者分母之间是否存在规律？若是都没有，则考虑反约分。有约分的分数数列是考查较多的一点，考生在反约分的时候要注意结合前后项分子分母之间的增减趋势进行反约分，使得反约分之后的数字与前后项形成同一个趋势。若是随意进行约分，容易费力不讨好，浪费时间。

3.幂次数列

数列特征：题干数字本身或附近出现幂次数

解题思路：转化为熟悉的平方或者立方数

（2014江苏B）1、121、441、961、1681、（   ）

A.2401

B.2601

C.3721

D.4961

解题思路：数列之中出现熟悉的平方数121=11的平方，又因为1=1的平方，441=21的平方，推测接下来的数字应为31的平方，41的平方，验证之后符合。则所求应为51的平方=2601。故本题答案为B。

（2015江苏）99、143、195、255、323、（）

A.353

B.366

C.398

D.399

解题思路：数列起伏较小，优先考虑做差。做差后得到新数列：44、52、60、68、（76），为公差是8的等差数列，则下一项应为68+8=76，所求项应为323+76=399。故本题答案为D。

幂次数列一般题干中数字的起伏相对较大，数列中出现幂次数或者幂次数附近的数字。考生在做题时可将题干数字转换成简单幂次数列或者经过加减修正转换成幂次数列，以此规律快速解题。关于幂次数列，要求考生对于常见的平方数和立方数要熟记于心，对于此类数据有一个敏感度。尤其要注意64这个数字，因为其本身具有既是平方数又是立方数的特性，是省考考查幂次数列中考频最高的数字。

4.做商数列

数列特征：数字之间出现明显倍数关系；

解题思路：两两做商；

（2014江苏B）1/2，1，3，15，120，（）

A.240

B.360

C.144

D.1440

解题思路：观察数列中的数字有明显的倍数关系，前后两两做商，得到2，3，5，8，做差为1，2，3，因此，做商之后的数列下一项为12。下一项为120×12=1440。故本题正确答案为D。

做商数列则考查的比较简单，倍数关系明显易算，难度较低，一般考生在此类题目上也比较容易拿分。

5.图形数列

数列特征：题干为图形形式

解题思路：凑中心数、大数或者相同数

（2015年广东省）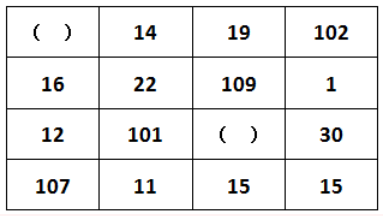

A. 11 7

B. 13 5

C. 17 9

D. 21 3

解题思路：按照一行一列观察表格，每行之间数字差距不大，考虑做和。每一行数字加和之后为148，每一列数字加和之后也为148。按照此规律，第一个数字应为148-14-19-102=13。只有B项符合，故正确答案为B。

本站声明:网站内容来源于网络,如有侵权,请联系我们,我们将及时处理。