考得多还简单?竟然会有这种知识点!
来啦来啦!我又来往你们脑子里灌知识点啦!和昨天一样,今天我们还是来讲一个考频比较高、拿分比较快的考点,它就是——钟表问题。小粉笔总结了一下总结了2015~2019年各省的题量,这个考点一般每年考查6~7道,且呈上涨趋势。而这类问题的正确率却没有想象中的那么高,但实际上钟表问题并不难,难度和工程问题差不多,只要我们掌握了做题技巧,它就是我们上岸的有力帮手!接下来,我们就一起做几道题,看看在实战中该如何解决这类问题。
基础知识类问题
例题

某单位实行弹性工作制,不严格规定上下班时间,但是上班打卡时间与下班打卡时间差应不少于9小时。某天上午小刘单位打卡时,从镜子里看到时钟显示如右图。则小刘当天最早的下班打卡时间为?
A.18:05
B.18:35
C.12:05
D.17:55

【解析】
已知“上班打卡时间与下班打卡时间差应不少于9小时”,比如粉笔是弹性工作制,8点上班,至少上班9小时,则下班时间最少是17点。问最早下班,则上班时间为9小时,镜子中钟表的时间如图,假设镜子后有个小人,从后面看就是正确的时间,或者把讲义翻页,从后面看也是正确的时间,考场上试卷的质量都不如粉笔的好,比较透,翻过来就能看出正确的时间,原理可以追溯到小学二年级,镜子中看到的物体是实际物体的对称,因此可以画个对称轴,将时钟对称过来,左边的时钟就是真实的时间,标出4个关键数字12、3、6、9,再标出数字11,此时分针指向11,时针指向9,有同学认为是9:55,9:55很接近10:00,因此时针应该指向很接近10的位置,而这里时针指向9,因此应该是8:55,8:55+9=17:55,D项当选。【选D】

【注意事项】
有同学认为时针不容易看,只看分针也是可以的,分针好看,指向11,则是55分,55分+9个整点还是55分,根据分针直接选择D项。
例题

小王早上看到挂钟显示8点多,急忙赶往公司上班。但是到了公司却发现时间和自己出门看到的挂钟时间一样,才明白是自己出门前误把挂钟的时针看成分针、分针看成时针。已知小王平时上班路程不超过1.5小时,今天上班他花费了( )
A.48分钟
B.55分钟
C.1小时
D.1小时3分钟
【解析】
读完题,老师也有同样的经历,小学是7点上课,看到时钟是6点25分,赶快出门,到街上一看没人,到学校门口也没人,门也没开,又回家,到家发现还是6点25分,才知道出门的时候是5点半。再看题,小王上班路程不超过1.5小时,问今天上班花费了多久,小王出门时看反时针分针,钟表时针分针看反是8点多,则已知出门时间是?点40多分,到公司是8点?分,已知平时上班路程不超过1.5小时,则出门时间可能是6点40多或者7点40多。假设是6点40多出发,此时时针在6~7之间,分针在8~9之间,反过来之后可知到公司时是8点30多,差值几乎是2个小时,这种情况在路上的时间超过1.5小时,因此不可能是6点40多出发,只能是7点40多出发,此时时针在7~8之间,分针在8~9之间,到公司时时针分针反过来看,是8点35多,中间相差不到1小时,排除C、D项,假设晚出发一会儿,7点45分出发,早到一会儿,8点35分到公司,7点45分~8点35分已经相差50分钟,这个假设相当于晚走了几分钟,早到了几分钟,则路上的时间超过50分钟,B项当选。【选B】


相关知识点
1、时间:一天等于24小时,1小时等于60分钟,1分钟等于60秒。
2、钟表:一天时钟转2圈(12小时是1圈),1小时时针走30度(时针指向12,走一小时指向1,相当于走了1大格,360°/12大格=30°),1分钟时针走0.5度(1小时走60分钟,30°/60=0.5°);1小时分针走360度(1小时分针走1圈),1分钟分针走6度(1小时有60分钟,360°/60=6°)。
例题

钟表的时针和分针在4点多少分第一次重合:

【解析】
题目问的是钟表的时针和分针在4点多少分第一次重合,每分钟时针走0.5°,分钟走6°,每分钟分针比时针多走6°-0.5°=5.5°,大家就记住这个结论即可,先看4点钟,画一下4点钟,前面我们说过一个大格是30°,这里有4个大格,所以4点的时候分针和时针之间是120°,假设到某一时刻重合,老师用蓝色笔画一下,分针也走到这里,时针从短的红线走到短的蓝线这里,分针从长的红线走到长的蓝线这里,从4点钟到重合的时候分针比时针多走了4点钟时的度数,也就是120°,接下来就用到结论,每分钟分针比时针多走5.5°,结果就是120°/5.5°=(120°*2)/(5.5°*2)=240/11=21+,结合选项,对应B项。【选B】
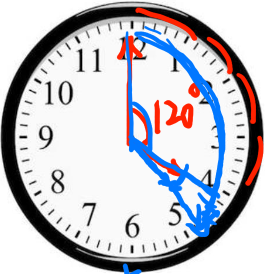
【注意事项】
1、每分钟时针走0.5°,分针走6°,每分钟分针比时针多走5.5°。
2、结论:把这两个结论记住会使用就可以。
(1)分针每分钟走6°,时针每分钟走0.5°,分针与时针旋转角度的倍数关系永远是6°/0.5°=12倍。
(2)每分钟分针比时针多走5.5°
知识点:特殊角度规律
1、24小时内,时针和分针成90°有44次(3、9、15、21点各重复一次)。1小时比如说是1点钟,从1点钟到2点钟这个时间内成90°有几次,就看1点到2点,我们画一下,假如说走到图中这个时刻出现第一次直角,再往后走度数越来越大,再出现直角的时候,就是当分针绕道时针的后面的时候,这里还能再成一次90°,所以在1点到2点之内能够成2个90°,前半小时有一次,后半小时有一次,1个小时有2次90°,按道理来说,24小时应该有48次,但是不是有48次,因为有重复,3点钟会发生重合,因为3点钟第一次是3:00,和2点钟第二次2:60是重合的,它俩其实是一次,但是我们算了两次,同样9点也重复算了一次,第一次9:00和8点的第二次8:60也重复了,既然3点和9点有重复,对于24小时制,3点可以理解为15点,9点可以理解为21点,总共有4次重复,所以应该用48-4=44次。

2、24小时内,时针和分针成180°有22次(6、18点各重复一次)。还是1点钟,1点钟到2点钟,结合常识想一想成180°有几次,一圈是360°,要成180°只有一次机会,按道理来说,24小时应该有24次,但是又有重复,6点的180°是6:00,和5点的180°是5:60,发生一次重复,同样,24小时制,18点也重复了,所以是有2次重复,就用24-2=22次。
3、24小时内,时针和分针成360°有22次(12、24点各重复一次)。360°就是重合了,1小时有一次,按道理来说,24小时应该有24次,但是有重复,12点会发生重复,12:00和11:60发生重复,同样,24小时制,24点也重复了,所以是有2次重复,就用24-2=22次。
快慢钟比例问题
【注意事项】
类似于比例行程问题,公式s=v*t,时间一定,速度变大,路程也变大,即t相同时,s和v成正比。
【知识点】
1、识别:出现快慢时钟,调整到标准时间后,求某个具体时间。
2、原理:比例行程——经过t相同,s和v成正比。
3、方法:
(1)找到速度之比。
(2)找到其中一个路程。
(3)根据比例得到另一个路程转化为钟表时间。
例题

已知一个时钟,每小时慢2分钟,下午14时整将时钟调至标准时间,当时钟走到18时50分时,标准时间为:
A.18时58分20秒
B.18时59分40秒
C.19时整
D.19时1分
【解析】
快慢钟、同一起点出发,t相同,s和v成正比,标准时钟一小时走60分钟,慢钟一小时走60-2=58分钟,路程从14点走到18点50分,走了4*60+50=290分钟。60/58=?/290,?=60*5=300分钟=5小时,起点是整点,经过是整点,所以结果也是整点,对应C项。【选C】
快慢钟追及(环形追及)问题
【知识点】
1、识别:出现快慢时钟,调整到标准时间后,求经过多长时间再显示标准时间。快慢钟求的是具体时间,快慢钟追及求的是经过多长时间同时显示标准时间。
2、原理:环形追及——S差=V差*T。
3、方法:
(1)求单个时钟显示相同时间:t=多走一圈的时间/速度差。
(2)求多个时钟所需t的最小公倍数。
例题

某收藏家有三个古董钟,时针都掉了,只剩下分针,而且都走得较快,每小时分别快2分钟、6分钟及12分钟。如果在中午将这三个钟的分针都调整指向钟面的12点位置,多少小时后这3个钟的分针会指在相同的分钟位置?
A.24
B.26
C.28
D.30
【解析】
本题没有提到标准时间,因为这个钟没有时针,所以本题只研究分针。公式:s差=v差*t,分针走一圈路程差为60分钟,速度差直接求即可。假设三个钟为A、B、C钟,A、B钟:t1=多60分钟÷多4分钟/小时=15小时,B、C钟:t2=多60分钟÷多6分钟/小时=10小时,15和10的最小公倍数为30,对应D项。【选D】
【知识点】
1、计算最小公倍数,可以短除,或者根据选项排除。
2、路程差一圈,如果时针分针都在,以时针为准,一圈12小时;如果只剩分针,以分针为准,一圈60分钟。
知识点总结
基础知识
1、认识钟表:时钟一天24小时转2圈,一圈360°;一圈包含12个大格、60个小格;每小时时针走30°,分针走360°;每分钟时针走0.5°,分针走6°,秒针走360°
2、速度关系:时针、分针旋转角度比为1:12;分针、秒针旋转角度比为1:60,每分钟分针比时针多走5.5°。
3、位置关系:
(1)24小时内,时针和分针成90°有44次(3、9、15、21点各重复一次)。
(2)24小时内,时针和分针成180°有22次(6、18点各重复一次)。
(3)24小时内,时针和分针成360°有22次(12、24点各重复一次)。
快慢钟比例问题
1、识别:出现快慢钟,调整到标准时间后,求某个具体时间。
2、原理:比例行程——经过t相同,s和v成正比。
3、方法:
(1)找到速度之比。
(2)找到其中一个路程。
(3)根据比例得到另一个路程转化为钟表时间。
快慢钟追及问题
1、识别:出现快慢时钟,调整到标准时间后,求经过多长时间再显示标准时间。
2、原理:环形追及——S差=V差*T。
3、方法:
(1)求单个时钟显示时间相同:t=多走一圈的时间/速度差。
(2)求多个时钟所需t的最小公倍数。
同学们有没有全部做对呢?快举手接受我的表扬~
本站声明:网站内容来源于网络,如有侵权,请联系我们,我们将及时处理。