两点式解决函数最值问题
函数最值问题虽不是常规热门题型,但在近几年的国、联考中常以经济利润问题的形式出现,此类题目套路性强,考生通过学习可快速掌握。今天粉笔与大家一起来了解一下,如何通过两点式快速解决函数最值问题。
此类题目中的方程为两括号相乘的形式,如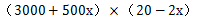 ,式子展开是一个抛物线的形式,展开之后有一个x²,当两端等于0的时候,中间对称轴对应最高点。这是使用两点式解决函数最值问题的原理,如果无法理解原理也没关系,只需要知道核心公式是
,式子展开是一个抛物线的形式,展开之后有一个x²,当两端等于0的时候,中间对称轴对应最高点。这是使用两点式解决函数最值问题的原理,如果无法理解原理也没关系,只需要知道核心公式是 ;第一步,令这2个括号等于0,解出
;第一步,令这2个括号等于0,解出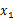 、
、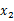 ;第二步,求出中间数
;第二步,求出中间数 ,这个时候的数对应的就是最高点。下面粉笔通过几道例题来为大家详细讲解一下两点式的具体应用。
,这个时候的数对应的就是最高点。下面粉笔通过几道例题来为大家详细讲解一下两点式的具体应用。
题型特征:单价和销量一升一降,问何时总价(总利润)最高
解决方法:两点式
1.设提价次数是 x,令总价(总利润)为 0,解得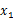 、
、
2.当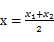 时,取得最值
时,取得最值
3.回归问题,根据要求的问题代入x计算
例1.【2019青海】某企业设计了一款工艺品,每件的成本是70元,为了合理定价,投放市场进行试销。据市场调查,销售单价是120元时,每天的销售量是100件,而销售单价每降价1元,每天就可多售出5件,但要求销售单价不得低于成本。则销售单价为多少元时,每天的销售利润最大?
A. 100元
B. 102元
C. 105元
D. 108元
【解题思路】设降价x(≤50)元,总利润为y,根据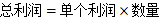 ,得
,得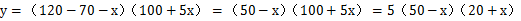 ,令
,令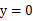 ,解得
,解得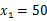 、
、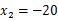 ,当
,当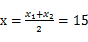 时,y取得最大值,即售价为
时,y取得最大值,即售价为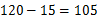 元时,利润最大,正确答案为C。
元时,利润最大,正确答案为C。
【粉笔点评】这种题在近几年考查的特别多,出现频率很高。典型的可以用两点式解决的函数最值问题,通过公式设立方程为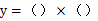 的形式后,令2个括号等于0,解出
的形式后,令2个括号等于0,解出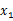 、
、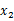 ,求出中间数
,求出中间数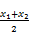 ,即可快速解题。
,即可快速解题。
例2.【2018联考】某苗木公司准备出售一批苗木,如果每株以4元出售,可卖出20万株,若苗木单价每提高0.4元,就会少卖10000株。问在最佳定价的情况下,该公司最大收入是多少万元?
A. 60
B. 80
C. 90
D. 100
【解题思路】假设在原价基础上提价x次,则共提高0.4x元,少卖了10000x株,即x万株。根据题意可得方程,收入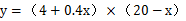 ,令
,令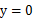 ,解得
,解得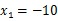 、
、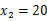 ,当
,当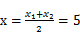 时,y取得最大值
时,y取得最大值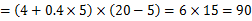 万元,正确答案为C。
万元,正确答案为C。
【粉笔点评】与例1不同的是,本题需求总收入,因此通过两点式确定了提价次数后,需要再代入原方程中求解总收入。另外在计算6×15时,容易错算成80;粉笔提醒考生要注意把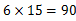 、
、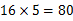 这两个式子区分开来,不要弄反。
这两个式子区分开来,不要弄反。
例3.【2018广州】某单位计划在户外举办讲座,计划使用72米的隔离带围成一个长方形作为活动场所,其中一边不封闭(即成 形),缺口面向讲坛。能围成的场所面积最大是( )平方米。
形),缺口面向讲坛。能围成的场所面积最大是( )平方米。
A. 324
B. 648
C. 972
D. 1296
【解题思路】设隔离带围成的场所宽为x米,面积为y平方米,则长为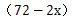 米。
米。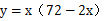 。令
。令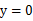 ,解得
,解得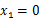 、
、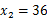 ,当
,当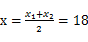 时,y取得最大值
时,y取得最大值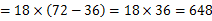 平方米,正确答案为B。
平方米,正确答案为B。
【粉笔点评】本题虽不是经济利润问题,但方程也是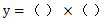 的形式,也可用两点式解题。另外计算时因选项尾数不同,也可采用尾数法快速锁定答案。
的形式,也可用两点式解题。另外计算时因选项尾数不同,也可采用尾数法快速锁定答案。
通过上面的题目可以发现,最终列出的式子都是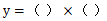 的形式, 所以函数最值问题的核心在于两个括号相乘的形式中,一个量在增长,一个量在减少,求乘积的最值。粉笔认为只要掌握了这一方法,函数最值问题即可迎刃而解。
的形式, 所以函数最值问题的核心在于两个括号相乘的形式中,一个量在增长,一个量在减少,求乘积的最值。粉笔认为只要掌握了这一方法,函数最值问题即可迎刃而解。
本站声明:网站内容来源于网络,如有侵权,请联系我们,我们将及时处理。